SpeeDe3DGS: Speedy Deformable
3D Gaussian Splatting with
Temporal Pruning and Motion Grouping

Dynamic extensions of 3D Gaussian Splatting (3DGS) achieve high-quality reconstructions through neural motion fields, but per-Gaussian neural inference makes these models computationally expensive.

Building on DeformableGS, we introduce Speedy Deformable 3D Gaussian Splatting (SpeeDe3DGS), which bridges this efficiency–fidelity gap through three complementary modules: Temporal Sensitivity Pruning (TSP) removes low-impact Gaussians via temporally aggregated sensitivity analysis, Temporal Sensitivity Sampling (TSS) perturbs timestamps to suppress floaters and improve temporal coherence, and GroupFlow distills the learned deformation field into shared SE(3) transformations for efficient groupwise motion.

On the 50 dynamic scenes in MonoDyGauBench, integrating TSP and TSS into DeformableGS accelerates rendering by 6.78× on average while maintaining neural-field fidelity and using 10× fewer primitives. Adding GroupFlow culminates in 13.71× faster rendering and 2.53× shorter training, surpassing all baselines in speed while preserving superior image quality.

Neural motion fields in dynamic 3D Gaussian Splatting (3DGS) enable highly detailed reconstructions, but per-Gaussian neural inference at every frame limits real-time performance. Speedy Deformable 3D Gaussian Splatting (SpeeDe3DGS) bridges this efficiency–fidelity gap through three complementary modules that jointly reduce redundant inference, stabilize temporal consistency, and distill neural motion into compact rigid representations:

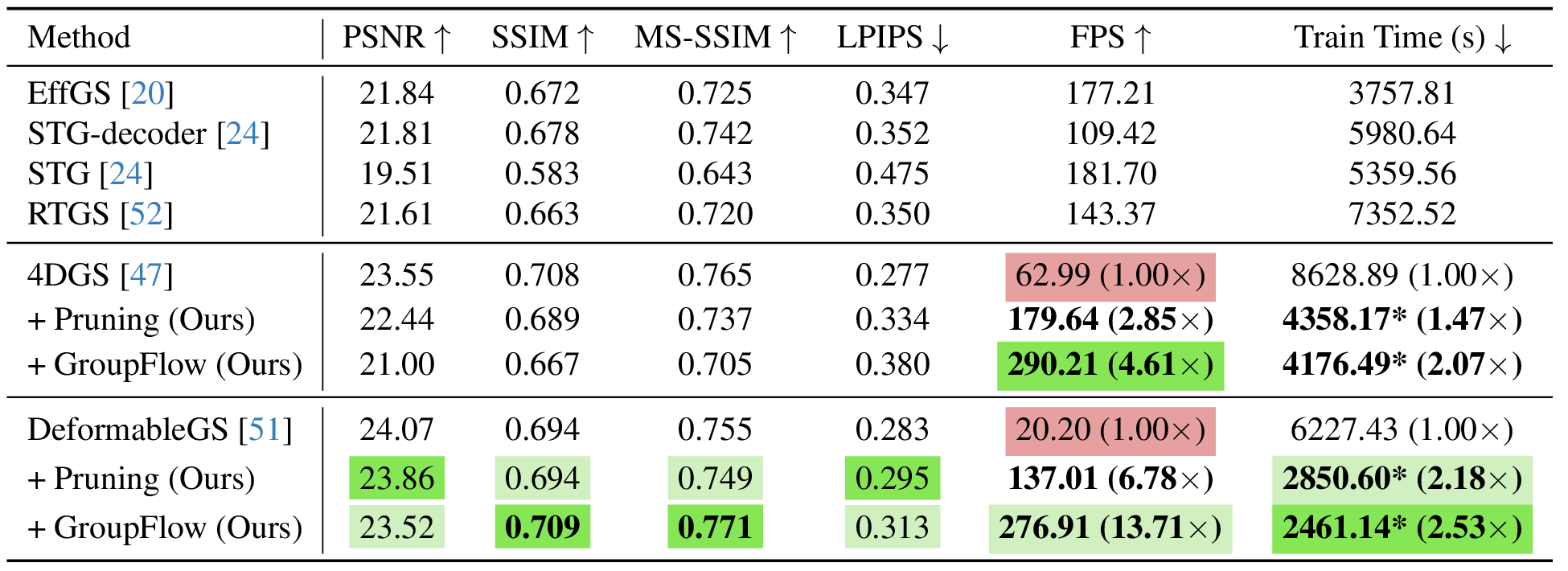
1. Temporal Sensitivity Pruning (TSP) removes redundant Gaussians by aggregating their gradient sensitivity across both space and time.
2. Temporal Sensitivity Sampling (TSS) enhances pruning stability by perturbing timestamps during sensitivity estimation, suppressing floaters and improving temporal coherence.
3. GroupFlow clusters Gaussians with similar motion trajectories, replacing per-Gaussian deformations with shared groupwise SE(3) transformations.

Implemented on top of Deformable 3D Gaussians, SpeeDe3DGS reduces redundant primitives, stabilizes temporal pruning, and lowers deformation cost — achieving neural-field fidelity at rendering speeds comparable to non-neural motion models.

For each Gaussian \(\mathcal{G}_i\), we calculate a Temporal Sensitivity Pruning (TSP) score \(\tilde{U}_{\mathcal{G}_i}\), which approximates its second-order sensitivity to the \(L_2\) loss across all training views: \[ \tilde{U}_{\mathcal{G}_i} \approx \nabla_{g_i}^2 L_2 \approx \sum_{\phi, t \in \mathcal{P}_{gt}} \left( \nabla_{g_i} I_{\mathcal{G}_t}(\phi) \right)^2, \] where \(g_i\) is the value of \(\mathcal{G}_i\) projected onto image space, \(\mathcal{P}_{gt}\) denotes the set of training poses and timesteps, and \(I_{\mathcal{G}_t}(\phi)\) is the rendered image at pose \(\phi\) and timestep \(t\).

Since deformation updates vary acrosss timesteps, these gradients are inherently time-dependent and capture the second-order effects of each Gaussian and its deformations on the dynamic scene reconstruction. As such, \(\tilde{U}_{\mathcal{G}_i}\) reflects each Gaussian's cumulative contribution to the scene reconstruction over time. We periodically prune low-contributing Gaussians during training, thereby reducing the neural inference load and boosting rendering speed.

While TSP identifies redundant Gaussians, it relies on gradients from discrete training frames. This may overlook floaters — unstable Gaussians that appear static in observed views but drift at unseen timestamps. To address this, Temporal Sensitivity Sampling (TSS) introduces temporal perturbation during sensitivity estimation by jittering the timestamp input to the deformation field:

\[ (\mu + \Delta\mu, r + \Delta r, s + \Delta s) = \mathcal{D}(\mu, r, s, t + \mathcal{N}(0,1)\beta\Delta t(1 - i/\tau)) \]

This temporally jittered sampling reveals unstable primitives early in training, encouraging robust pruning and suppressing floaters. The noise magnitude decays linearly (annealing), ensuring precise reconstruction in later stages. Together, TSP and TSS improve temporal smoothness and enable up to 11× fewer Gaussians with comparable image quality to the unpruned baseline.

Even after pruning, dynamic 3D Gaussian Splatting requires predicting a deformation for every Gaussian, which remains computationally expensive. GroupFlow addresses this by distilling the learned neural motion field into grouped SE(3) transformations that capture locally coherent motion.

Given a dense deformable 3DGS model, each Gaussian \(\mathcal{G}_i\) is represented as a sequence of mean positions \(\mathcal{M}_i = \{\mu_i^t\}_{t=0}^{F-1}\) across \(F\) timesteps. We initialize \(J\) control trajectories \(\{h_j^t\}\) via farthest point sampling at \(t=0\), and assign each \(\mu_i\) to the most similar \(h_j\) using trajectory similarity score:

$$ S_{i,j} = \lambda_r \, \mathrm{std}_t(\| \mu_i^t - h_j^t \|) + (1-\lambda_r) \, \mathrm{mean}_t(\| \mu_i^t - h_j^t \|). $$

We then fit a group-wise SE(3) trajectory to each group \(\mathcal{M}^j\) by aligning sampled means over time. To predict the deformation of \(\mu_i \in \mathcal{M}^j\) at timestep \(t\), we apply a learned SE(3) transformation relative to its control point:

$$ \mu_i^t = R_j^t (\mu_i^0 - h_j^0) + h_j^0 + T_j^t. $$

The shared flow parameters \(\{h_j^0, R_j^t, T_j^t\}\) are optimized jointly with the scene. This formulation distills dense, per-Gaussian neural deformations into a smaller set of groupwise SE(3) motions, reducing the number of transformations per frame from \(N\) (per Gaussian) to \(J\) (per group).

As a result, GroupFlow achieves substantial acceleration during both training and rendering while maintaining temporally coherent, high-quality motion reconstruction. Beyond efficiency, this distillation regularizes the learned motion field, smoothing noisy trajectories and improving robustness in real-world dynamic scenes.